oreohd.blogg.se - Angle of reflection ellipse

Spheroid, the ellipsoids obtained by rotating an ellipse about its major or minor axis.

Ellipsoid, a higher dimensional analog of an ellipse.

Einstein's contributions to modern physics may not have been discovered if it were not for ellipses. The general solution for a harmonic oscillator in two or more dimensions is also an ellipse, but this time with the origin of the force located in the center of the ellipse.Īlbert Einstein also used the ellipse to prove his theory of relativity by using an elliptical shaped mass. More generally, in the gravitational two-body problem, if the two bodies are bound to each other (i.e., the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. Later, Isaac Newton explained this fact as a corollary of his law of universal gravitation. For any ellipse's point the angles between the normal to the ellipse at this point. point and the straight lines drawn from the ellipse foci to the point are congruent. Therefore, the point such that is minimum is the intersection point of and. For any ellipse's point the angles between the tangent line to the ellipse at this. For any point on the line, we have, and thus. Ellipse Reflection Radius Unwrapper 2. Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses. Solution to problem 1: Let be the reflection point of over the line. Angle-Side-Side Pythagorean Visualization. Since no other curve has such a property, it can be used as an alternative definition of an ellipse. Then all rays are reflected to a single point - the second focus.

The inverse function, the angle subtended as a function of the arc length, is given by the elliptic functions.Īssume an elliptic mirror with a light source at one of the foci. More generally, the arc length of a portion of the circumference, as a function of the angle subtended, is given by an incomplete elliptic integral. If an ellipse is not centered at the origin of an x- y coordinate system, but again has its major axis along the x-axis, it may be specified by the equation Which use the trigonometric functions sine and cosine. Hope you learnt equation of normal to ellipse in all forms, learn more concepts of ellipse and practice more questions to get ahead in the competition.The same ellipse is also represented by the parametric equations: Y = mx \(\mp\) \(\)) which is the required condition. The equation of normal to the given ellipse whose slope is ‘m’, is Since the angle of incidence equals the angle of reflection. Hence, normal to given ellipse is 8x + 6y = 14. Light emanating from one focus of an elliptic mirror will pass through the other focus.

The normal to given ellipse in point form is \(a^2x\over x_1\) + \(b^2y\over y_1\) = \(a^2-b^2\) This program provides a geometric proof that a reflected ray from a focus in an ellipse passes through the other focus. The Equation of normal to the given ellipse at (\(x_1, y_1\)) is

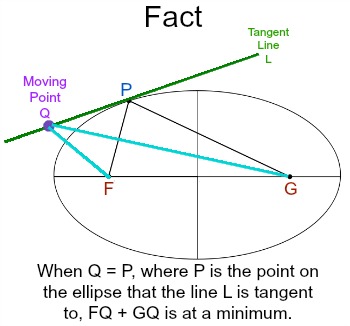
Let a be the length of the semimajor axis of the ellipse.

An ellipse also has directices and important reflection properties. stating that the angle of incidence is equal to the angle of reflection in optics.) Proof. Equation of Normal to ellipse : \(x^2\over a^2\) + \(y^2\over b^2\) = 1 (a) Point form : Figure 1: An ellipse in the Cartesian plane.